Stock Return Prediction

Predicting the sign of stock returns in a noisy time series tabular dataset

Figure 1: Technical analysis of stock 1

Challenge Goals

This project is based on a Data Challenge by QRT that aims at predicting the return of a stock in the US market using historical data over a recent period of 20 days. The one-day return of a stock j on day t with price P_j^t (adjusted from dividends and stock splits) is given by:

\( R_{j}^{t} = \frac{P_{j}^{t}}{P_{j}^{t-1}} - 1 \)

In this challenge, we consider the residual stock return, which corresponds to the return of a stock without the market impact. Historical data are composed of residual stock returns and relative volumes, sampled each day during the 20 last business days (approximately one month). The relative volume V_j^t at time t of a stock j among the n stocks is defined by:

\( \overline{V}_{j}^{t} = \frac{V^{t}}{\text{median}(\{V_{j}^{t-1}, \ldots, V_{j}^{t-20}\})} \)

\( V_{j}^{t} = \overline{V}_{j}^{t} - \frac{1}{n} \sum_{i=1}^{n} \overline{V}_{i}^{t} \)

where V^{t} is the volume at time t of a stock j. We also give additional information about each stock such as its industry and sector.

The metric considered is the accuracy of the predicted residual stock return sign.

Data Description

The dataset comprises 46 descriptive features (all float/int values):

DATE: an index of the date (the dates are randomized and anonymized so there is no continuity or link between any dates),
STOCK: an index of the stock,
INDUSTRY: an index of the stock industry domain (e.g., aeronautic, IT, oil company),
INDUSTRY_GROUP: an index of the group industry,
SUB_INDUSTRY: a lower level index of the industry,
SECTOR: an index of the work sector,
RET_1 to RET_20: the historical residual returns among the last 20 days (i.e., RET_1 is the return of the previous day and so on),
VOLUME_1 to VOLUME_20: the historical relative volume traded among the last 20 days (i.e., VOLUME_1 is the relative volume of the previous day and so on).

The target variable is the sign of the residual stock return at time t (binary). The dataset contains 418,595 observations for training and 198,429 observations for testing.

Feature Engineering

To enhance the dataset and improve prediction accuracy, the following feature engineering techniques were applied:

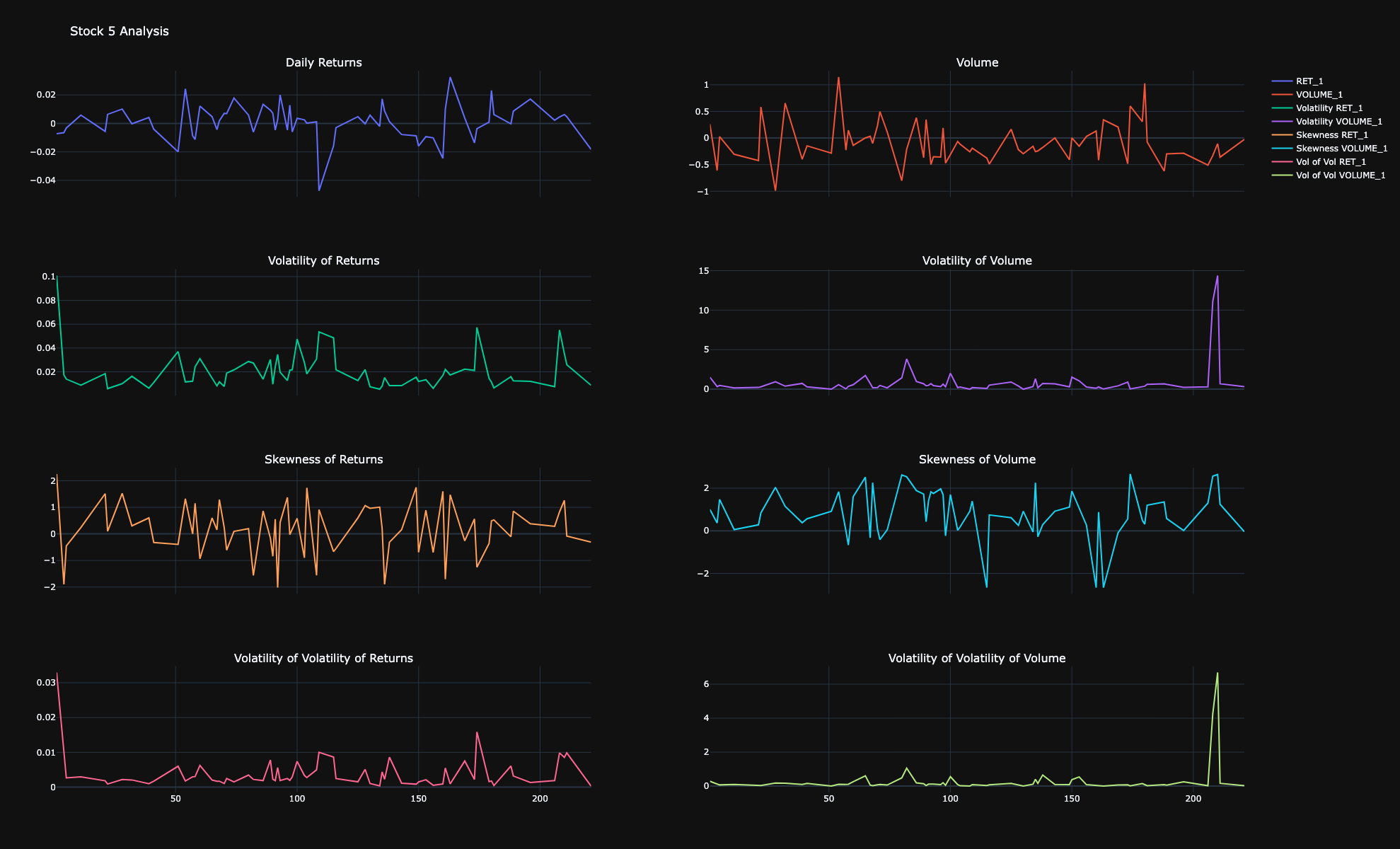
Volatility Measures

Rolling Standard Deviation:

\( \text{Rolling Std} = \sqrt{\frac{1}{n-1} \sum_{i=1}^{n} (R_i - \overline{R})^2} \)

Volatility of Volatility (Vol of Vol) (std of std):

\( \text{Vol of Vol} = \sqrt{\frac{1}{n-1} \sum_{i=1}^{n} (\sigma_i - \overline{\sigma})^2} \)

Figure 2: A look into volatility of stock 5

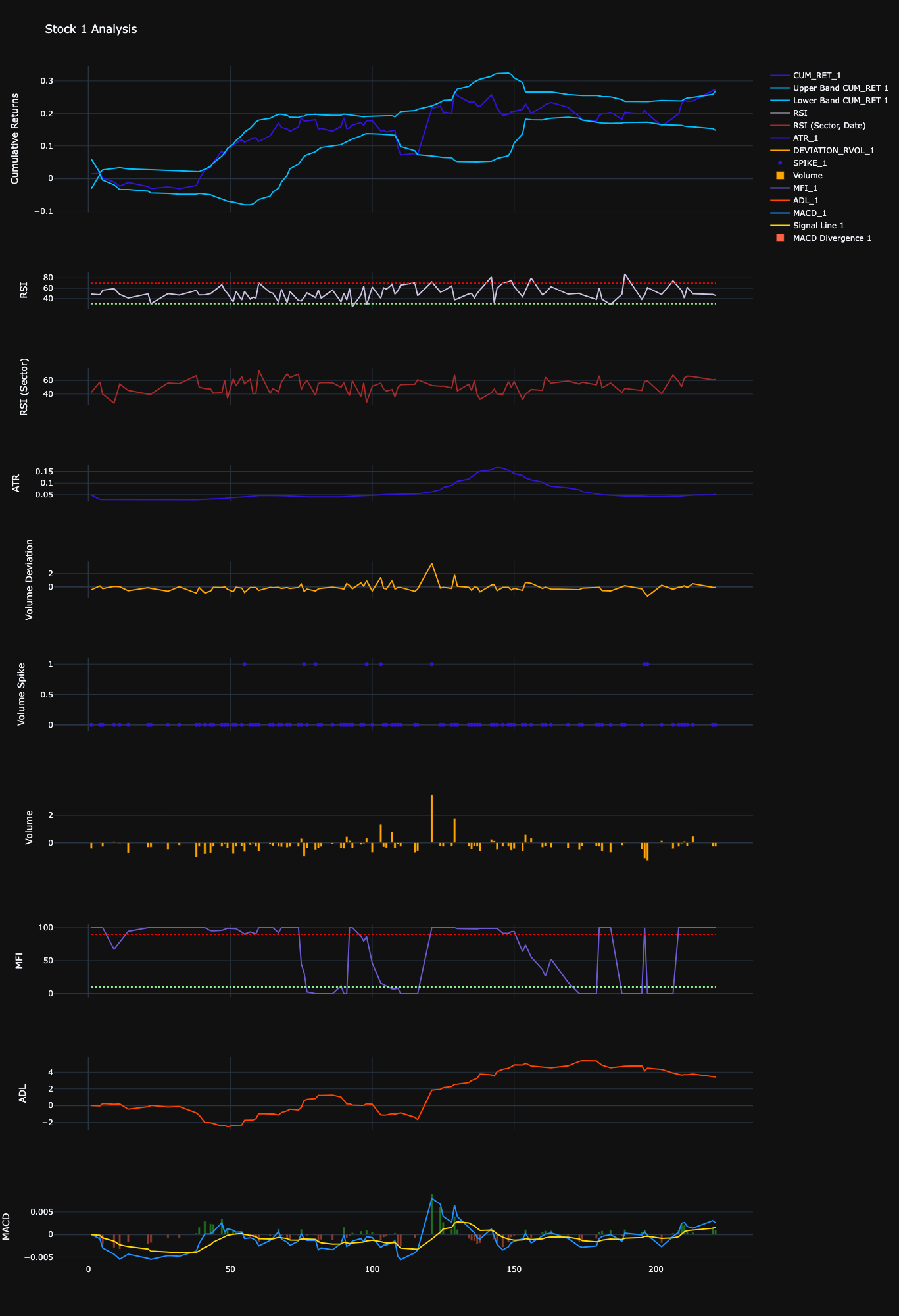
Technical Indicators

Money Flow Index (MFI):

\( \text{MFI} = 100 - \left( \frac{100}{1 + \frac{\sum(\text{Positive Money Flow})}{\sum(\text{Negative Money Flow})}} \right) \)

Relative Strength Index (RSI):

\( \text{RSI} = 100 - \left( \frac{100}{1 + \frac{\text{Average Gain}}{\text{Average Loss}}} \right) \)

Accumulation/Distribution Line (ADL):

\( \text{ADL} = \sum \left( \frac{(C - L) - (H - C)}{H - L} \times V \right) \)

Average True Range (ATR):

\( \text{ATR} = \frac{1}{n} \sum_{i=1}^{n} \text{TR}_i \)

Moving Average Convergence Divergence (MACD):

\( \text{MACD} = \text{EMA}_{12} - \text{EMA}_{26} \)

Implementation Structure

Data Cleaning and Preprocessing

Addressing missing values
Deciding how to drop missing values depending on important features (RET_1 to RET_5)
Deciding how to fill missing values (because of outliers, median is favored over mean)

Exploratory Data Analysis (EDA)

Having a look at the distributions of the stocks' RET_i and VOLUME_i
Having a look at the distribution of the aggregated SECTOR and INDUSTRY's RET_i and VOLUME_i

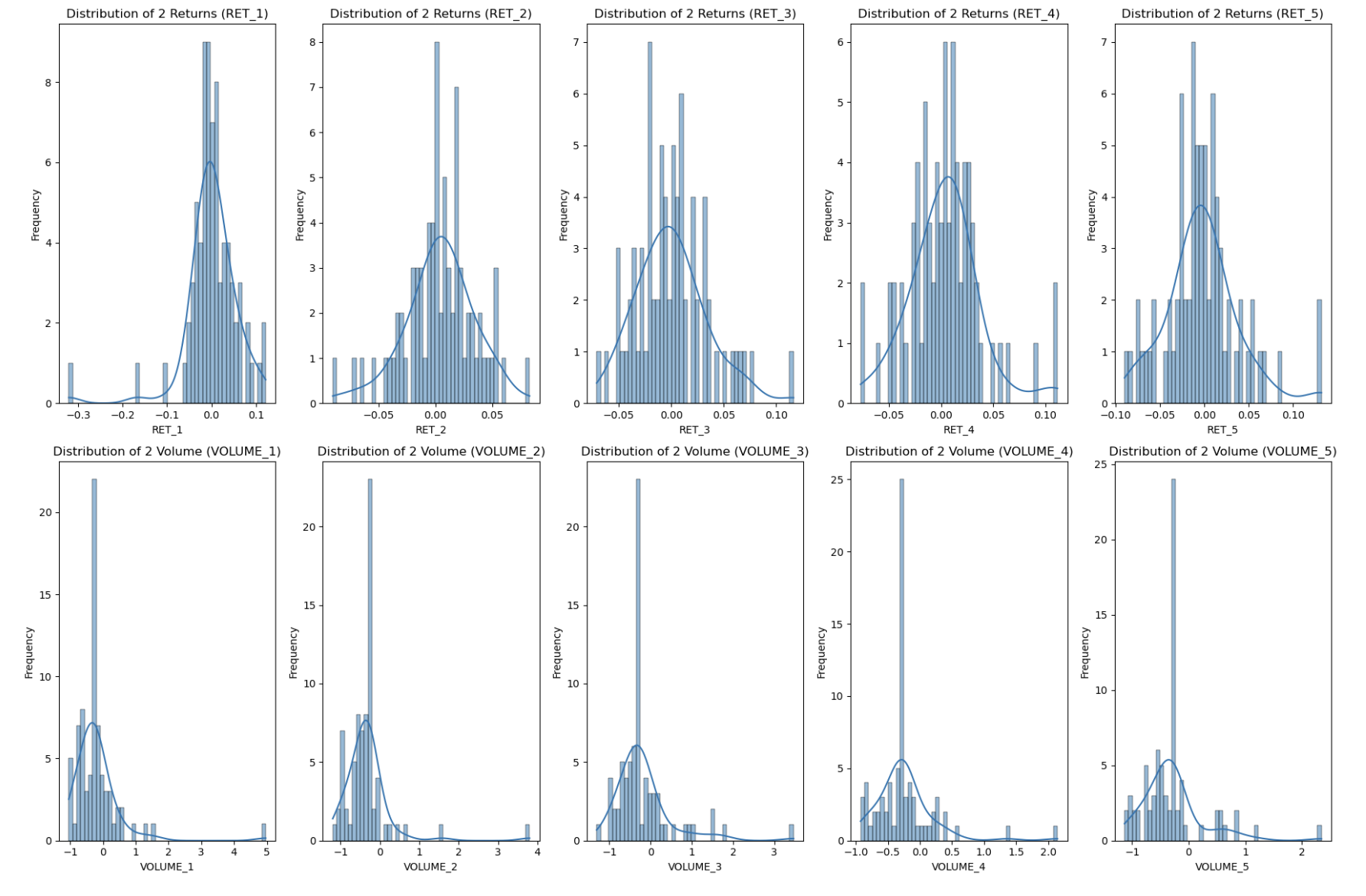
Figure 3: A look into stock 2 distribution

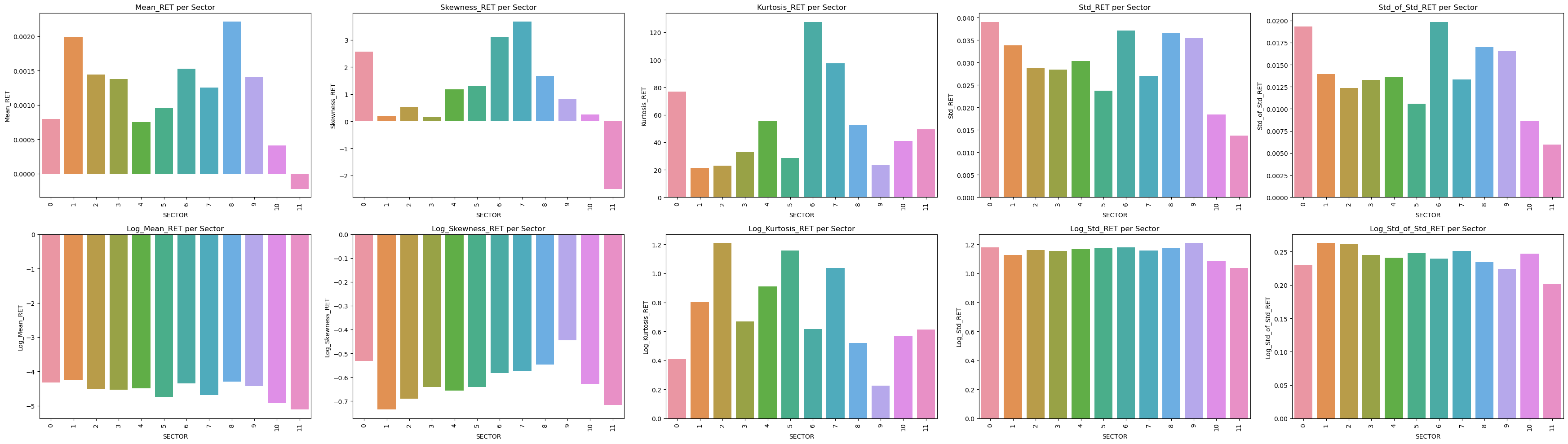
Figure 4: A look into distributions of sectors

Advanced Feature Engineering

Technical Indicators: To extract information from our dataset, technical indicators have been coded. These are typical technical indicators that can also be found in the TA-Lib library:

Figure 5: Technical analysis of stock 1 with RET_5 focus

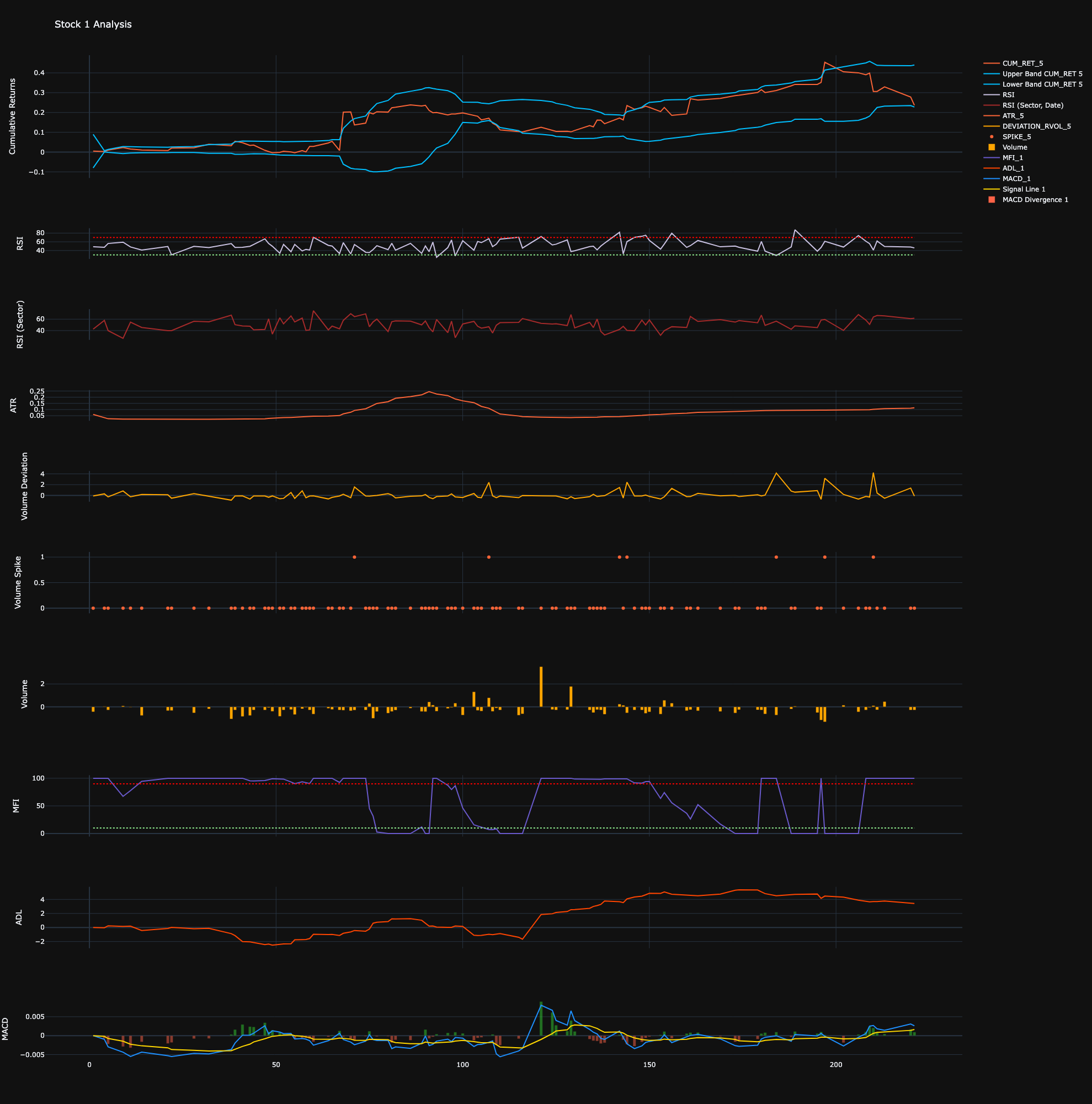
Volatility Indicators: Volatility (Std), Volatility of Volatility (std of std) per stock and per sector and per stock adjusted per sector.

Statistical Indicators: To extract more information, factor investing techniques were considered. The approach involved calculating Principal Components per SECTOR and INDUSTRY (aggregated per stock category), both whitened and not whitened. These didn't have as much positive impact in terms of explainability of the target variable RET as the Technical Indicators.

Prediction Model

The model is a Random Forest applied with stratified cross-validation, to ensure proper assessment and avoid overfitting to any training part of the dataset.

Results

Outcome: In the leaderboard, this approach achieved the 70th position out of 399 submissions, placing in the top 17.3% percentile of submissions.

Future Work

Future ideas include:

Leveraging kurtosis and skewness of the distributions for statistically-driven feature engineering and indicators
Exploring more statistically and mathematically proven and robust methods to derive alpha
Investigating ensemble methods and advanced ML techniques

Resources

GitHub Repository