N-Body Simulation
Efficient N-body Simulation Using Parallel Computing
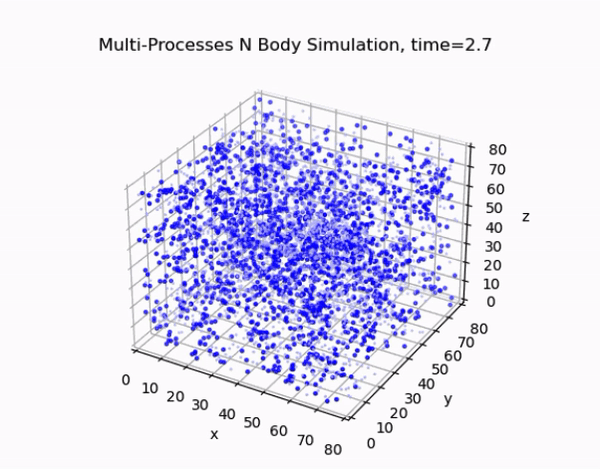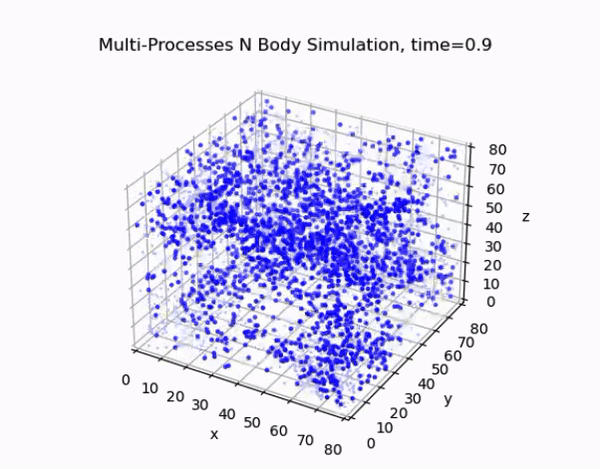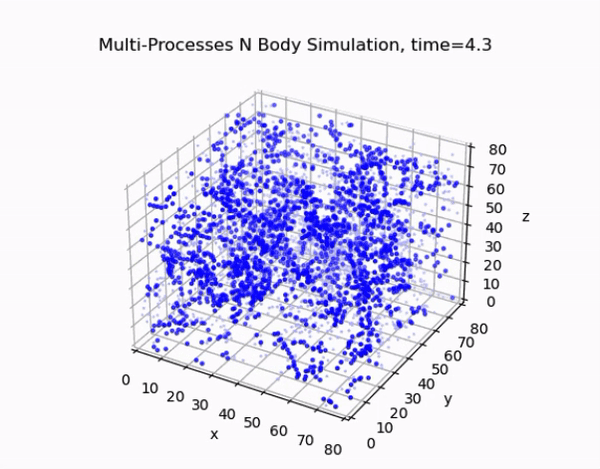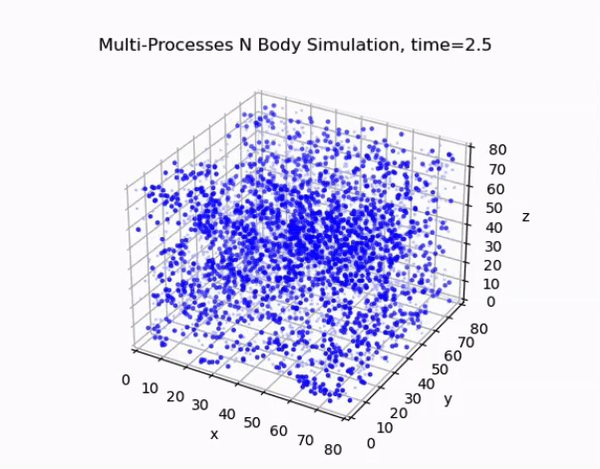
Overview
This project focuses on developing an efficient and accurate N-body simulation system using high-performance computing techniques. The N-body problem is crucial in fields like astrophysics, cosmology, and aerodynamics, involving the simulation of the motion of a system of particles under the influence of gravitational forces.
Key Objectives
- Algorithm Development: Create an N-body simulation algorithm that can be parallelized efficiently.
- Optimization: Reduce communication overhead and load balancing issues in the parallelization process.
- High-Performance Implementation: Implement the simulation on a high-performance computing architecture to handle large-scale systems.
- Scalability: Investigate and ensure the scalability of the developed algorithm.
Methodology
- Cell Lists Algorithm: Utilizes a grid of cells to reduce computational complexity by focusing on local interactions.
- Leapfrog Time Integration: Ensures accurate propagation of particle positions and velocities.
- Parallelization Techniques: Combines OpenMP for parallel processing within nodes and MPI for communication between nodes.
- Performance Analysis: Conducts roofline and scaling analyses to evaluate the efficiency and scalability of the algorithm.
Technical Implementation
Cell Lists Algorithm
The cell lists algorithm divides the simulation domain into a regular grid of cells. Each particle is assigned to a cell based on its position, and force calculations are performed only between particles in neighboring cells. This approach reduces the computational complexity from O(N²) to O(N) for sufficiently large systems.
Leapfrog Integration
The leapfrog integration scheme is used for time evolution of the particle system. This method provides good energy conservation properties and is well-suited for molecular dynamics simulations. The integration alternates between updating velocities and positions:
- Update velocities at half-time step using current forces
- Update positions using the new velocities
- Calculate new forces
- Update velocities for the second half-time step
Parallel Computing Strategy
The parallelization strategy employs a hybrid approach:
- OpenMP: Used for shared-memory parallelization within compute nodes
- MPI: Used for distributed-memory parallelization across compute nodes
- Domain Decomposition: The simulation domain is partitioned among processes to balance computational load
Performance Analysis
Roofline Analysis
The roofline model was used to analyze the performance characteristics of the algorithm, identifying computational bottlenecks and memory bandwidth limitations. This analysis helped optimize the code for different hardware architectures.
Scaling Studies
Strong and weak scaling studies were performed to evaluate the algorithm's efficiency as the number of processors increases. The results demonstrate good scalability up to a certain number of processors, after which communication overhead becomes the limiting factor.
Findings
- Efficiency Gains: The parallelized algorithm demonstrates significant improvements in computation time compared to serial implementations.
- Scalability: The algorithm scales well with the number of processors, though efficiency decreases with increased communication overhead at very high processor counts.
- Load Balancing: Dynamic load balancing techniques help maintain efficiency as particle distributions evolve during the simulation.
Conclusion
The project successfully develops a highly scalable and efficient N-body simulation system, advancing the computational techniques available for simulating large-scale particle interactions. The hybrid parallelization approach and optimized algorithms enable the simulation of complex gravitational systems with good performance characteristics.